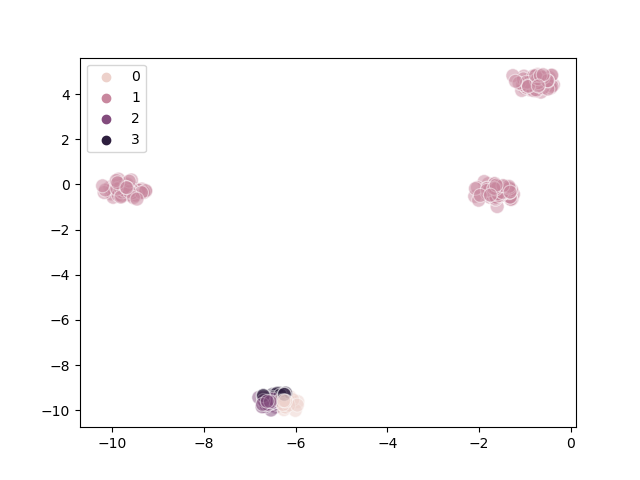
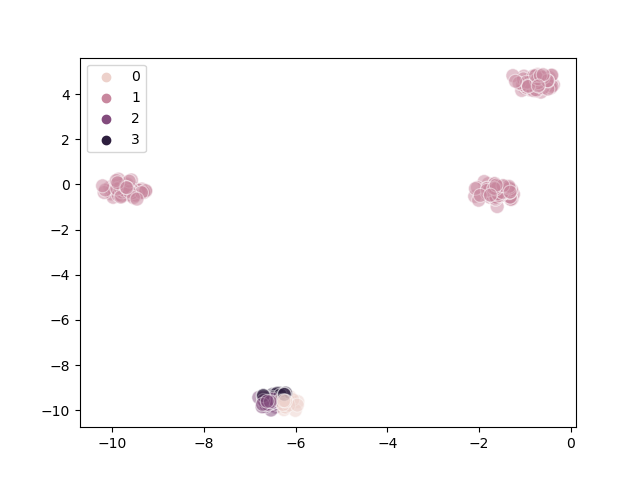
K-Means clustering: Implmentation and Analysis

After reading about the section K-Means Clustering in the book, I decided to implement naive (vanilla) K-Means clustering by myself.

Here’s what I did. (some details omitted for brevity, you can find my full implementation as a Jupyter Notebook on Kaggle)

def kmeans(
    X,
    centers: int,
    *,
    tolerance: float,
    max_iter: int,
    random_state: int | None = None,
):
    rng = np.random.default_rng(random_state)
    centroids = rng.choice(X, size=centers, replace=False)

    for n in range(max_iter):
        # Determine the closest centroid for each data point
        closest_centroid = np.array(
            [np.argmin([np.linalg.norm(x - c) for c in centroids]) for x in X]
        )

        # Update the centroids
        new_centroids = [
            np.mean(X[closest_centroid == i], axis=0) for i in range(centers)
        ]

        # Loop until we are done
        if np.allclose(centroids, new_centroids, atol=tolerance):
            break

        centroids = new_centroids

    return closest_centroid, centroids

However, today’s focus is not on how I implemented the algorithm, as my code above is mostly (hopefully) self-explanatory, but on the analysis of the execution results. In case you are unfamiliar with the algorithm, you can find a Wikipedia article on K-Means here.

Analysis

In total, I ran the K-Means algorithm on generated data with 2, 3, 4 and 5 clusters, and a cluster_std of 0.2, 1.0, 1.8 and 2.6 (determines how diffuse the generated points are). For each of the combinations, I configured a random_state of 0 through 19, so as to avoid the effect of randomness on the results.

General Performance

The following table shows the performance of the algorithm on each of the configurations

# of clusters cluster_std	2	3	4	5
0.2	A	B(0.35)	B(0.4)	C
1.0	A-	B(0.2)	B(0.25)	B(0.45)
1.8	A-	B-(0.15)	B-(0.15)	B-
2.6	A-	B-	B-	B-

Note

• grades

  • A: excellent

  • B: good (error rate less than 0.5)

  • C: poor

• annotations

  • “-”: has overlap problem

  • “(error_rate)”: estimated error rate shown in parentheses

We can infer from the plot that:

1. As the number of clusters increases, the performance of K-Means generally goes down

   Possible explanation: K-Means rely on random selection of initial centroids. The more clusters, the less likely the centroids are evenly distributed among the actual clusters.

2. As cluster_std increases, the error rate goes down

   Possible explanation: It becomes easier for the centroid to jump between clusters as cluster_std increases. (See section Steps)

3. As cluster_std increases, the problem of overlap becomes more significant

   Possible explanation: High cluster_std makes it easy for clusters to overlap with each other.

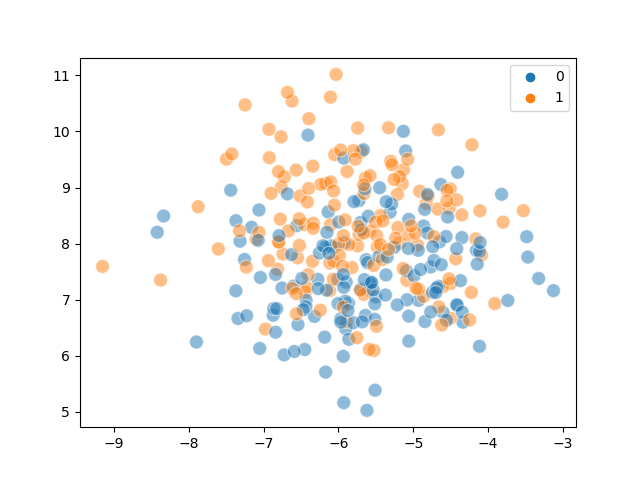
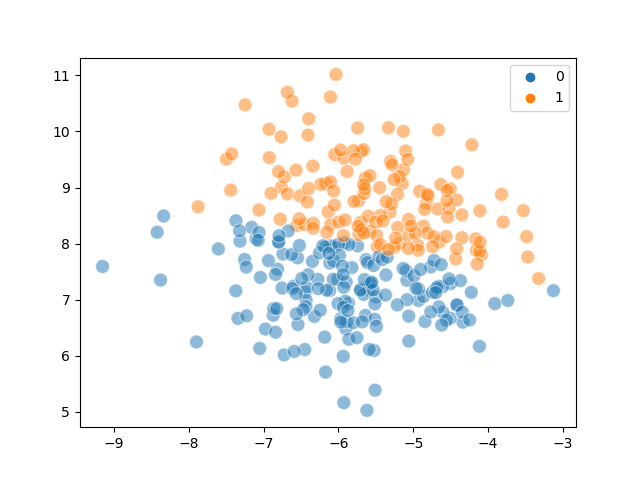
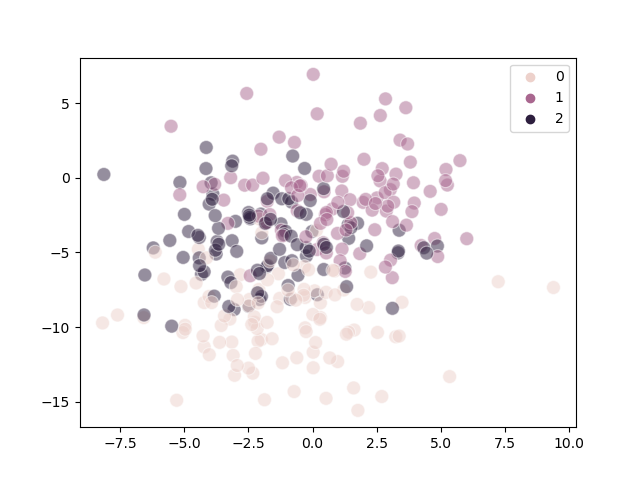
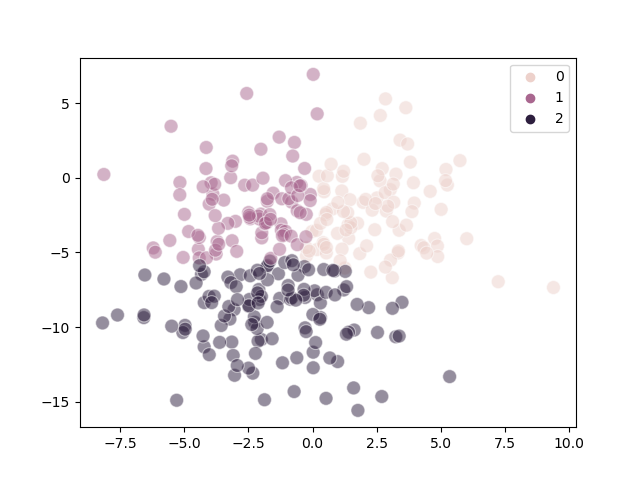
Overlap

When clusters become too close to each other, they overlap. This makes it extremely hard for clustering algorithms to separate the clusters. (The same problem exists for supervised classification)

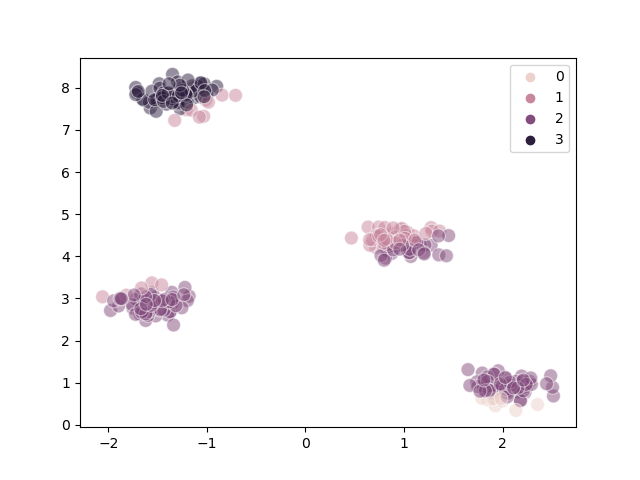
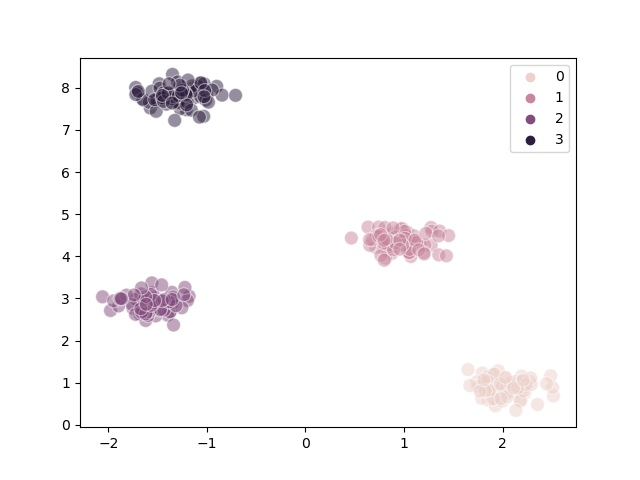
The following diagrams demonstrate the overlap problem:

Actual	Predicted

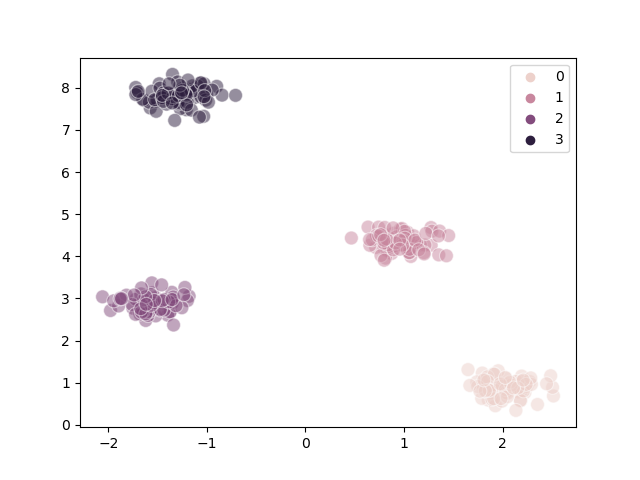
Steps

We can visualize the individual steps the K-Means algorithms made during the clustering process.

The following is a well-clustered example:

Steps	Diagram
1
2
3

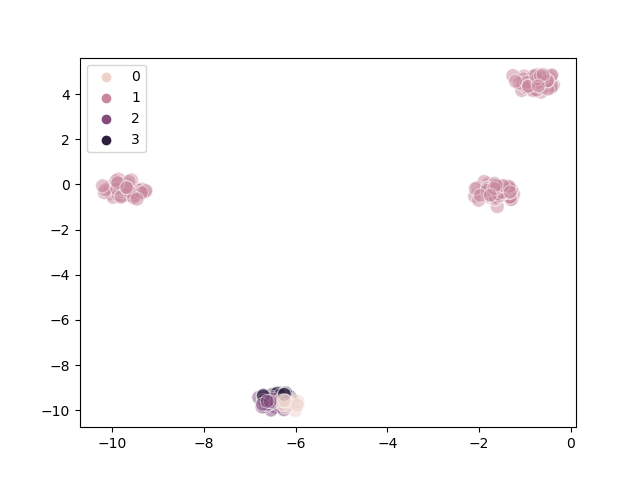
The following is a poorly-clustered example:

Steps	Diagram
1
2
3

We can infer from the diagrams that:

1. Poor clustering probably results from poor initial choice of centroids

2. The algorithm converges quite quickly

Empty cluster

It is possible that empty clusters will appear during the algorithm (as stated in the book), and I indeed got a warning for that:

/opt/conda/lib/python3.10/site-packages/numpy/core/fromnumeric.py:3432: RuntimeWarning: Mean of empty slice.
  return _methods._mean(a, axis=axis, dtype=dtype,
/opt/conda/lib/python3.10/site-packages/numpy/core/_methods.py:182: RuntimeWarning: invalid value encountered in divide
  ret = um.true_divide(

Afternote

There are three main() functions in the notebook. You can select from them to generate the diagrams in this blog post. What each of them does is implementation detail and will not be explained in this post.

Conclusion

The K-Means algorithm is an incredibly efficient algorithm and can perform clustering tasks with great accuracy as long as the initial centroids and number of clusters are well-chosen.

Enlarging one’s vocabulary   Matrix Calculus Demystified