\[ \newcommand{\sym}[1]{\mathrm{#1}} \newcommand{\conc}[1]{\left[\mathrm{#1}\right]} \newcommand{\h}{\sym{H^+}} \newcommand{\hho}{\sym{H_2O}} \newcommand{\hhho}{\sym{{H_3O}^+}} \newcommand{\oh}{\sym{{OH}^-}} \newcommand{\ph}{\mathrm{pH}} \newcommand{\pka}{\mathrm{p}K_a} \newcommand{\arsinh}{\mathop{\rm arsinh}\nolimits} \]

A Quantitative Analysis of the pH Titration Curve for Monoprotic Acids

In introductory college chemistry textbooks, the pH curve for a weak acid-strong base titration is often shown as follows:

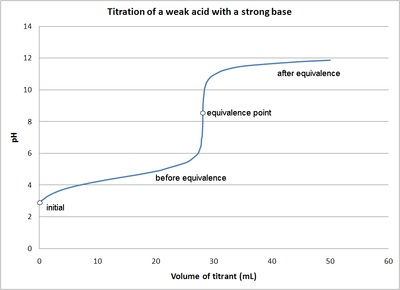
Figure used with the permission of J.A. Freyre under the Creative Commons Attributions-Share Alike 2.5 Generic.

Its unique shape led me to wonder: what is the underlying equation? In particular, is the equivalence point also an inflection point of the pH curve?

In mathematical terms, is it true that

(1)\[ \frac{d^2\mathrm{pH}}{d(\text{Volume of titrant})^2} = 0\text{?} \]

In this article, I will attempt to answer this question by deriving the pH curve equations for:

1. monoprotic strong acid-strong base titrations

2. monoprotic weak acid-strong base titrations

The polyprotic versions are left to the reader as an exercise.

Strong Acid-Strong Base Titration

For the sake of simplicity, let’s assume the analyte is \(1\,L\) of \(1\,M\;\sym{HCl}(aq)\) and the titrant is \(\sym{NaOH}(aq)\). In an actual titration, the volume of the solution increases as the titrant is being added. The magnitude of this change in concentration caused by the increase in the volume, however, is small enough that we will neglect it for the rest of this article.

\[\begin{split} \hho &\rightleftharpoons \h + \oh \quad K_w = 1\times 10^{-14} \\ \sym{HCl} &\rightarrow \h + \sym{{Cl}^-} \\ \end{split}\]

Note that the autoionization equilibrium condition

(2)\[ K_w = \conc{\h}\conc{\oh} \]

stays true even as \(\sym{NaOH}(aq)\) is being added to the analyte.

The solution must have a net electric charge of zero:

(3)\[ \conc{Na^+} + \conc{\h} = \conc{Cl^-} + \conc{\oh} \]

Let \(x = \text{moles}\;\sym{NaOH} = \conc{Na^+}\). Solving for \(\conc{\oh}\) in (3) and and plugging the result into (2) gives

(4)\[\begin{split} \conc{\oh} &= \conc{\h} + x - 1 \\ K_w &= \conc{\h}\left(\conc{\h} + x - 1\right) \\ \end{split}\]

Solving for \(\conc{\h}\) gives

(5)\[\begin{split} \conc{\h} &= \frac{(1-x) + \sqrt{(1-x)^2 + 4K_w}}{2} \\ &= \sqrt{K_w}\left[\frac{1-x}{2\sqrt{K_w}} + \sqrt{\left(\frac{1-x}{2\sqrt{K_w}}\right)^2 + 1}\right] \\ \end{split}\]

Therefore

(6)\[\begin{split} \ph &= -\log\conc{\h} \\ &= -\log\sqrt{K_w} - \frac{1}{\ln 10}\cdot\ln\left[\frac{1-x}{2\sqrt{K_w}} + \sqrt{\left(\frac{1-x}{2\sqrt{K_w}}\right)^2 + 1}\right] \\ &= \frac{1}{2}\sym{p}K_w - \frac{1}{\ln 10}\arsinh{\frac{1-x}{2\sqrt{K_w}}} \\ &= \boxed{7 - \frac{1}{\ln 10}\arsinh\left(\frac{1-x}{2} \cdot 10^7\right)} \\ \end{split}\]

This is indeed the typical strong-acid titration graph:

Notice that because:

1. The inverse hyperbolic function \(\arsinh x\) is odd.

2. The function is shifted horizontally by \(1\) and vertically by \(7\).

The graph is indeed symmetric about the equivalence point \((1,\,7)\).

Weak Acid-Strong Base Titration

The situation gets more interesting if we consider a weak acid that ionizes only partially. We will use \(1\,M\;\sym{HF}(aq)\) as the example:

(7)\[\begin{split} \sym{HF} &\leftrightharpoons \h + \sym{F^-}\quad K_a = 6.8 \times 10^{-4} \\ K_a &= \frac{\conc{\h}\conc{F^-}}{\conc{HF}} \\ 1 &= \conc{F^-} + \conc{HF} \\ \end{split}\]

Similar to (3), we also have

(8)\[ \conc{Na^+} + \conc{\h} = \conc{F^-} + \conc{\oh} \]

However, we cannot plug in \(1\,M\) for \(\conc{F^-}\) as we did for \(\conc{Cl^-}\) in (3). Instead, we must write:

(9)\[ \conc{\oh} = \conc{\h} + x - \conc{F^-} \]

where \(\conc{F^-}\) can be determined from (7):

(10)\[ \conc{F^-} = \frac{K_a}{K_a + \conc{\h}} \]

Plugging everything into (2) gives:

(11)\[ K_w = \conc{\h}\left(\conc{\h} + x - \frac{K_a}{K_a + \conc{\h}}\right) \]

Equation (11) is cubic if we multiply by \(K_a + \conc{\h}\) on both sides. Instead of attempting to use the cubic formula, I decided to take a step back and directly analyze the derivatives of \(\ph\) so that I can answer my original question (1).

From (11) we have

(12)\[ \frac{K_w}{\conc{\h}} = \conc{\h} + x - \frac{K_a}{K_a + \conc{\h}} \]

Taking the derivative w.r.t \(x\) gives

(13)\[ -\frac{K_w}{\conc{\h}^2}\frac{d\conc{\h}}{dx} = \frac{d\conc{\h}}{dx} + 1 + \frac{K_a}{\left(K_a + \conc{\h}\right)^2}\frac{d\conc{\h}}{dx} \]

Rearranging and applying the chain rule gives

(14)\[\begin{split} 1 &= -\frac{d\conc{\h}}{dx}\left(1 + \frac{K_w}{\conc{\h}^2} + \frac{K_a}{\left(K_a + \conc{\h}\right)^2}\right) \\ &= -\frac{d\left(10^{-\ph}\right)}{dx}\left(1 + \frac{K_w}{\conc{\h}^2} + \frac{K_a}{\left(K_a + \conc{\h}\right)^2}\right) \\ &= -10^{-\ph}\cdot\ln 10\cdot\left(-\frac{d\ph}{dx}\right)\left(1 + \frac{K_w}{\conc{\h}^2} + \frac{K_a}{\left(K_a + \conc{\h}\right)^2}\right) \\ &= \frac{d\ph}{dx}\cdot\ln 10\cdot\left(\conc{\h} + \conc{\oh} + \frac{K_a\conc{\h}}{\left(K_a + \conc{\h}\right)^2}\right) \\ \end{split}\]

Thus

(15)\[ \boxed{\frac{d\ph}{dx} = \frac{1}{\ln 10}\left(\conc{\h} + \conc{\oh} + \frac{K_a\conc{\h}}{\left(K_a + \conc{\h}\right)^2}\right)^{-1}} \]

We can use slope fields to numerically solve for pH:

Note

GeoGebra fails to graph the function when \(\pka\) is outside the narrow range \((6.9,\,7.1)\). I believe it is due to numerical errors when the concentrations of ions are very small, leading to overflow/underflow. I will try to plot it using Python in an upcoming post, if possible.

A couple things to notice before we take the second derivative:

1. The graph indeed looks like the textbook diagram.

2. In (15), the term \(\conc{\h} + \conc{\oh} + \dfrac{K_a\conc{\h}}{\left(K_a + \conc{\h}\right)^2}\) can be logically broken down into two parts:

   1. \(\conc{\h} + \conc{\oh}\), which attains its minimum when \(\conc{\h} = \conc{\oh} = \sqrt{K_w}\)

   2. \(\dfrac{K_a\conc{\h}}{\left(K_a + \conc{\h}\right)^2}\):

      (16)\[\begin{split} \frac{K_a\conc{\h}}{\left(K_a + \conc{\h}\right)^2} &= \frac{1}{\frac{K_a}{\conc{\h}} + \frac{\conc{\h}}{K_a} + 2} \\ &\le \frac{1}{4} \\ \end{split}\]

      The maximum is only achieved when \(K_a = \conc{\h}\). Also note that if we plug in this condition into (7), we get

      (17)\[ \conc{HF} = \conc{F^-} \]

      which is exactly when the buffer capacity is maximized.

   Based on these observations, we can qualitatively explain the shape of the graph:

   1. Initially, term 2 is small because \(\conc{\h} \gg K_a\). Term 1 is also decently small because the acid is weak. As a result, \(\dfrac{d\ph}{dx}\) is large.

   2. As \(\oh\) is being added, term 2 starts to increase, reaching its maximum when \(\ph = \pka\) (Henderson–Hasselbalch + (17)), leading to a smaller \(\dfrac{d\ph}{dx}\).

   3. When sufficient amounts of \(\oh\) have been added, term 2 starts to decrease again. At the same time, term 1 is small because \(\ph\) is close to \(7\), corresponding to the sharp rise portion of titration.

   4. Excess \(\oh\): term 1 is large because of high \(\ph\), small \(\dfrac{d\ph}{dx}\).

The Second Derivative

Let

(18)\[ A = \conc{\h} + \conc{\oh} + \dfrac{K_a\conc{\h}}{\left(K_a + \conc{\h}\right)^2} \]

Therefore

(19)\[\begin{split} \frac{d\ph}{dx} &= \frac{1}{A\ln 10} \\ \frac{d^2\ph}{dx^2} &= -\frac{1}{A^2\ln 10}\frac{dA}{d\conc{\h}}\frac{d\conc{\h}}{dx} \\ &= -\frac{1}{A^2\ln 10}\left(1 - \frac{K_w}{\conc{\h}^2} + \frac{K_a\left(K_a - \conc{\h}\right)}{\left(K_a + \conc{\h}\right)^3}\right) \cdot 10^{-\ph}\cdot\ln 10\cdot\left(-\frac{d\ph}{dx}\right) \\ &= \frac{1}{A^3\ln 10}\left(\conc{\h} - \conc{\oh} + \frac{K_a\conc{\h}\left(K_a - \conc{\h}\right)}{\left(K_a + \conc{\h}\right)^3}\right) \\ \end{split}\]

When the equivalence point is reached,

(20)\[ x = 1 \]

which combined with (9) gives

(21)\[ \conc{\oh} = \conc{\h} + 1 - \frac{K_a}{K_a + \conc{\h}} \]

Thus

(22)\[\begin{split} \frac{d^2\ph}{dx^2}\Bigg|_{x = 1} &= \frac{1}{A^3\ln 10}\left(\conc{\h} - \conc{\h} - 1 + \frac{K_a}{K_a + \conc{\h}} + \frac{K_a\conc{\h}\left(K_a - \conc{\h}\right)}{\left(K_a + \conc{\h}\right)^3}\right) \\ &= \frac{1}{A^3\ln 10}\left(\frac{K_a\conc{\h}\left(K_a - \conc{\h}\right)}{\left(K_a + \conc{\h}\right)^3} - \frac{\conc{\h}}{K_a + \conc{\h}}\right) \\ &= \frac{1}{A^3\ln 10} \cdot \frac{\conc{\h}}{K_a + \conc{\h}} \cdot \left(\frac{K_a\left(K_a - \conc{\h}\right)}{\left(K_a + \conc{\h}\right)^2} - 1\right) \end{split}\]

which is obviously not equal to zero. The last term, however, is very small because \(K_a\) is much greater than \(\conc{\h}\) near the equivalence point.

Conclusion

The study of acid-base titrations is a fascinating subject. In this article, we have proven that the equivalence point is in fact, not the inflection point of a weak acid-strong base titration curve, contrary to our intuition. But what about polyprotic acids? What about weak bases? What will happen if we consider the change in volume?

Each of these questions (and many others) invites a studious, scientific, and fascinating discussion.

An Interesting Integral